Arrays: Models to Understanding

What is an array or “the area model?

A quantity or collection of objects arranged in rows and columns creating an area.

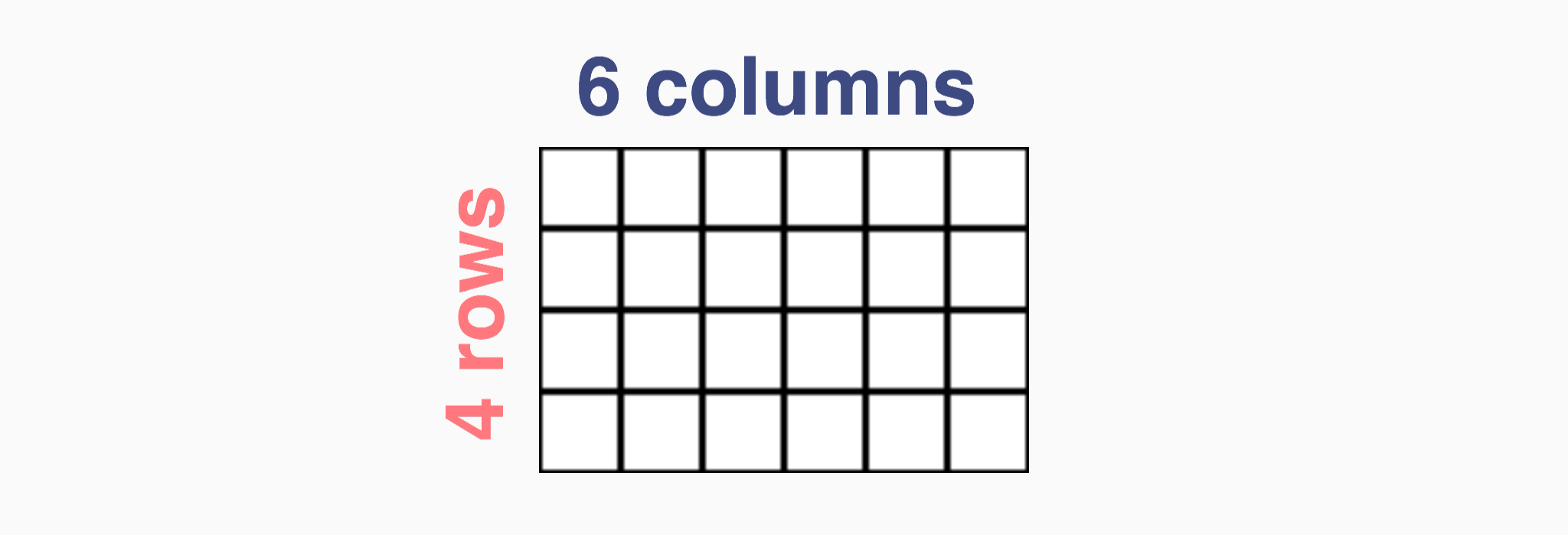
The above is a 4 x 6 array. 24 squares arranged in 4 rows of 6 (or 6 columns of 4 using the commutative property of multiplication.)

By building arrays or area models, kids are empowered to see multiplication as an operation they are able to manipulate and break down in order that they may find their solution. Teaching our students to utilize the properties of math gives them the authority and gumption to take risks when problem solving.

When building arrays with Math Stackers, if they try a solution that is not true, they will SEE what needs to be changed, instantly putting them on a path to finding a true solution.

What if you have students who have not “memorized their facts”? Building and manipulating multiplication combinations (arrays) is a great way for them to grasp the concept of multiplication and know that there is more than one way to get to the product than just knowing it off-hand. This number reasoning is a great skill that will benefit them their entire lives!

Let’s build and break apart 4 x 6 and then later 3 x 17. (To see a video tutorial of building arrays with Math Stackers, click here.)

4 x 6

Select four 6-blocks and arrange them with their notched sides in an array that is four rows by six columns.

Connect to the equation: 4 x 6 = ?

You may have students who instantly recognize that the product of this array is 24. You may also have students who do not...and that is totally okay! Encourage them to use something they DO know such as their multiples of 5…

“You know so much that you can use. How about your multiples of 5?”

Guide them to utilize this knowledge and build a partial array on top of the 4 x 6.

Connect to the equation: 4 x 6 = (4 x 5) + ?

This partial array allows students the opportunity to connect what else is needed to complete their 4 x 6 array. Build the remaining partial array.

Connect to the equation: 4 x 6 to 4(5 + 1) = (4 x 5) + (4 x 1)

20 + 4 = 24

Now that is some successful math thinking…they have successfully multiplied 4 x 6 by utilizing the distributive property in order to decompose the combination into smaller arrays that they know!

3 x 17

Create the array.

Connect to the equation: 3 x 17 = 3(10 +7)

A benefit of the design of Math Stackers is that this model already focuses on breaking apart 3 x 17 into 2 parts: 3 x 10 and 3 x 7. This is a great strategy considering our minds think so efficiently in groups of 10. Seeing and physically breaking apart 3 x 17 allows your students to think about multiplication in terms of areas.

Connect to the equation: 3(10 + 7) = (3 x 10) + (3 x 7)

30 + 21 = 51

The first area is 3 x 10….most of your students may be comfortable with this one and identify it as an area of 30. Some of your students may also be familiar with 3 x 7 and instantly identify it as 21.

However, you may have some students who are not familiar with this combination and sometimes this means they get stuck. But they don’t have to! Encourage them to break it down further into terms they know.

If this is what your students chose to try, they can see that the needed area to complete the 3 x 7 array is 3 more rows of 2…or a 3 x 2 array.

Connect to the equation: 3(10 + 5 + 2) = (3 x 10) + (3 x 5) + (3 x 2)

30 + 15 + 6 = 51

Through the power of the distributive property of multiplication your students have solved 3 x 17 by decomposing and composing the 3 x 17 array in a way that makes sense to them! As an educator, this is what I strive for….that my students are thinking mathematically and are empowered to make math work for them.

Want to try this with your kiddo(s)? Head over to our website and check out the Elementary Set. This set has the Math Stackers you need to build your own arrays.

Happy Math Stacking!